Now that we have learned about negation, conjunction, disjunction and the conditional, we can include the logical connector for each of these statements in more elaborate statements. In this lesson, we will learn how to determine the truth values of a compound statement with the logical connectors ~, 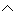 ,
, 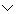 and
and  .
.
 Example 1:
Example 1:
| Given: | p: 72 = 49 | true |
| q: A rectangle does not have 4 sides. | false | |
| r: Harrison Ford is an American actor. | true | |
| Problem: | Write each sentence below in symbolic form. Then determine its truth value. | |
| 1. | If 72 = 49, then a rectangle has 4 sides. | p ~q ~q |
true |
| 2. | If 72 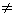 49, then a rectangle does not have 4 sides. 49, then a rectangle does not have 4 sides. |
~p q q |
true |
| 3. | If a rectangle has 4 sides, then Harrison Ford is not an American actor. | ~q ~r ~r |
false |
| 4. | If Harrison Ford is an American actor, then 72 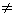 49. 49. |
r ~p ~p |
false |
| 5. | If 72 = 49 or a rectangle does not have 4 sides, then Harrison Ford is not an American actor. | (p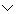 q) q) ~r ~r |
false |
In Example 1, each of the first four sentences is represented by a conditional statement in symbolic form. In item 5, (p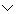 q)
q) ~r is a compound statement that includes the connectors
~r is a compound statement that includes the connectors 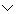 ,
,  , and ~. It is easier to determine the truth value of such an elaborate compound statement when a truth table is constructed as shown below.
, and ~. It is easier to determine the truth value of such an elaborate compound statement when a truth table is constructed as shown below.
| p | q | ~r | p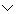 q q |
(p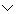 q) q) ~r ~r |
| T | F | F |
T |
F |
Example 2:
| Given: | p: 28 is a multiple of 7. | true |
| q: 7 is an even number. | false | |
| Problem: | Determine the truth value of this compound statement: ~p (q (q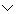 p) p) |
|
Solution:
| p | q | ~p | q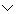 p p |
~p  (q (q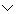 p) p) |
| T | F | F |
T |
T |
Example 3:
| Given: | a is true, b is false, and c is true. |
| Problem: | Determine the truth value of this compound statement: (~a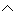 c) c) b b |
Solution:
| a | b | c | ~a | ~a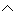 c c |
(~a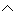 c) c) b b |
| T | F | T | F |
F |
T |
In the examples above, we were given the truth values of each sentence and asked to determine the truth value of the resulting compound statement. However, when we are not given this information, we need to construct a truth table. In each of the following examples, we will construct a truth table for the given compound statement in order to determine its truth values.
Example 4: What are the truth values of this compound statement? (p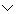 q)
q) q
q
| p | q | p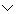 q q |
(p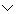 q) q) q q |
| T | T | T |
T |
| T | F | T |
F |
| F | T | T |
T |
| F | F | F |
T |
Solution: The truth values of (p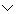 q)
q) q are {T, F, T, T}.
q are {T, F, T, T}.
Example 5: What are the truth values of this compound statement? q (p
(p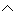 ~q)
~q)
| p | q | ~q | p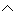 ~q ~q |
q (p (p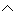 ~q) ~q) |
| T | T | F | F |
F |
| T | F | T | T |
T |
| F | T | F | F |
F |
| F | F | T | F |
T |
Solution: The truth values of q (p
(p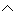 ~q) are {F, T, F, T}.
~q) are {F, T, F, T}.
Example 6: What are the truth values of this compound statement? (s r)
r)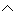 ~r
~r
| r | s | ~r | s r r |
(s r) r)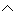 ~r ~r |
| T | T | F | T |
F |
| T | F | F | T |
F |
| F | T | T | F |
F |
| F | F | T | T |
T |
Solution: The truth values of (s r)
r)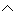 ~r are {F, F, F, T}.
~r are {F, F, F, T}.
Example 7: What are the truth values of this compound statement? ~b (a
(a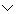 b)
b)
| a | b | ~b | a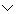 b b |
~b (a (a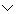 b) b) |
| T | T | F | T |
T |
| T | F | T | T |
T |
| F | T | F | T |
T |
| F | F | T | F |
F |
Solution: The truth values of ~b (a
(a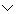 b) are {T, T, T, F}.
b) are {T, T, T, F}.
Summary: We have learned how to write a sentence as a compound statement in symbolic form. We have learned how to determine the truth values of a compound statement with the logical connectors ~, 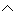 ,
, 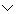 and
and  .
.

Exercises
Directions: Read each question below. Select your answer by clicking on its button. Feedback to your answer is provided in the RESULTS BOX. If you make a mistake, choose a different button.
| 1. |
|
|||||
| 2. | If r and s are false statements, then what is the truth value of (~r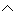 s) s) s? s? |
| 3. | If x and y are true statements, then what is the truth value of (x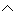 y) y) ~y? ~y? |
| 4. | What are the truth values of this statement? (~x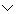 y) y) y y |
| 5. | What are the truth values of this statement? ~p (p (p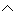 ~q) ~q) |




