Introduction to Decimals
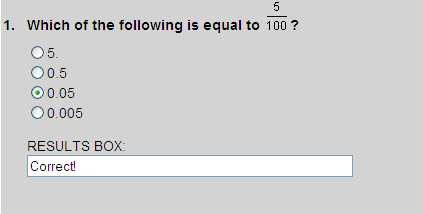
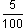 is shown in the place-value chart below.
is shown in the place-value chart below.
 |
 |
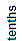 |
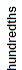 |
| 0 | . | 0 | 5 |
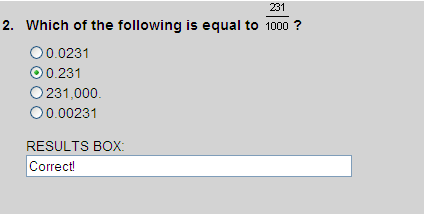
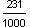 is shown in the place-value chart below.
is shown in the place-value chart below.
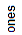 |
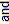 |
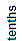 |
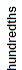 |
 |
| 0 | . | 2 | 3 | 1 |
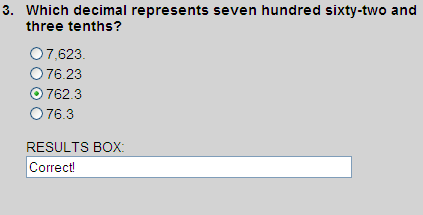
Seven hundred sixty-two and three tenths is shown in the place-value chart below.
 |
 |
 |
 |
 |
| 7 | 6 | 2 | . | 3 |
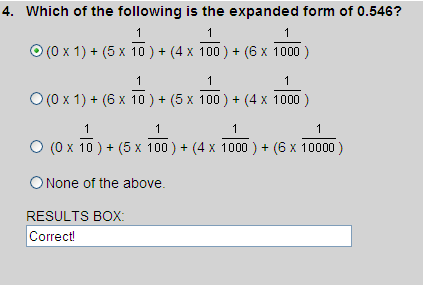
Expanded form is a way to write numbers by showing the value of each digit. The correct expanded form of 0.546 is choice 1. See the place-value chart below.
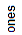 |
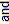 |
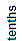 |
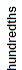 |
 |
| 0 | . | 5 | 4 | 6 |
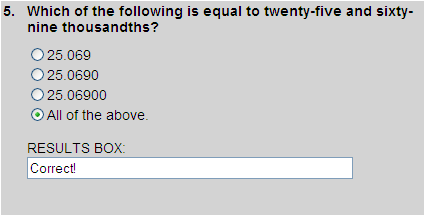
The decimals in the first three choices are equivalent decimals. So they are all equal to twenty-five and sixty-nine thousandths. These decimals are shown in the place-value chart below.
 |
 |
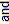 |
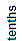 |
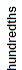 |
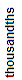 |
 |
 |
| 2 | 5 | . | 0 | 6 | 9 | ||
| 2 | 5 | . | 0 | 6 | 9 | 0 | |
| 2 | 5 | . | 0 | 6 | 9 | 0 | 0 |
Reading and Writing Decimals
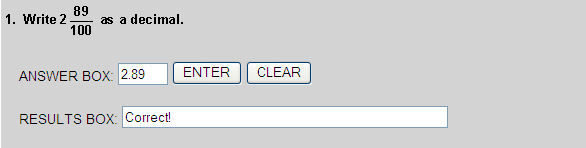
See the place-value chart below.
 |
 |
 |
 |
| 2 | . | 8 | 9 |
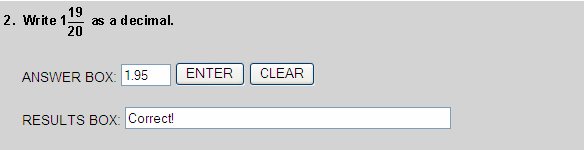
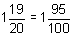
See the place-value chart below.
 |
 |
 |
 |
| 1 | . | 9 | 5 |
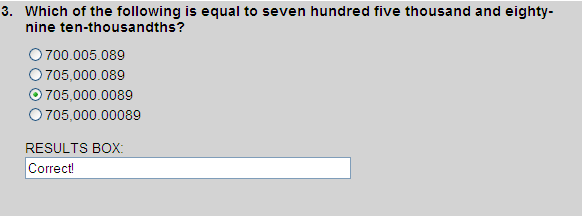
Seven hundred five thousand and eighty-nine ten-thousandths is shown in the place-value chart below.
 |
 |
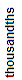 |
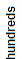 |
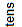 |
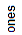 |
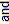 |
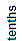 |
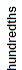 |
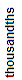 |
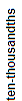 |
| 7 | 0 | 5 | 0 | 0 | 0 | . | 0 | 0 | 8 | 9 |
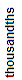 |
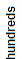 |
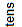 |
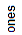 |
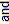 |
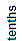 |
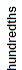 |
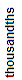 |
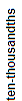 |
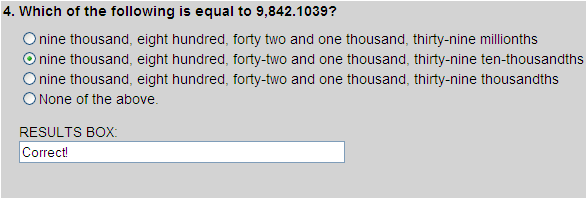
| 9 | 8 | 4 | 2 | . | 1 | 0 | 3 | 9 |
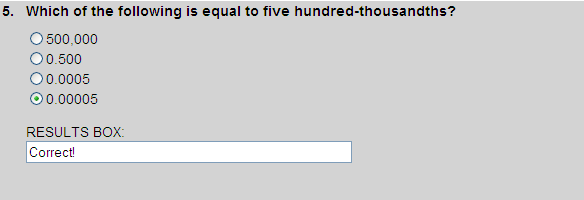
Five hundred-thousandths is shown in the place-value-chart below.
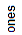 |
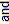 |
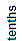 |
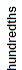 |
 |
 |
 |
| 0 | . | 0 | 0 | 0 | 0 | 5 |
Comparing Decimals
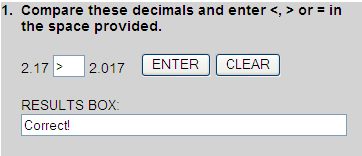
Writing one decimal below the other, we get:
2.170
2.017
Writing one decimal below the other, we get:
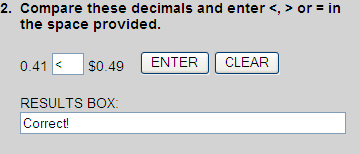
0.41
0.49
Writing one decimal below the other, we get:
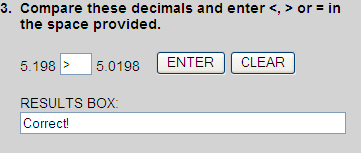
5.1980
5.0198
Writing one decimal below the other, we get:
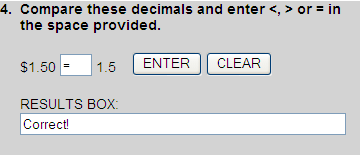
1.50
1.50
Writing one decimal below the other, we get:
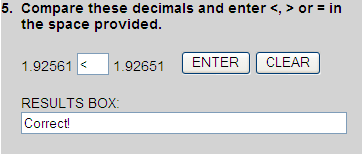
1.92561
1.92651
Ordering Decimals
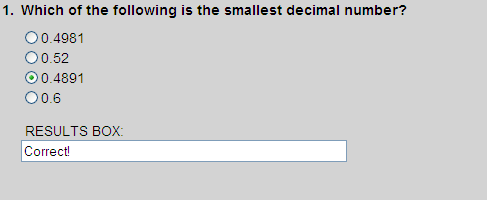
Writing one decimal beneath the other in their original order, we get:
0.4981
0.5200
0.4891
0.6000
Ordering these decimal from least to greatest, we get:
0.4891
0.4981
0.5200
0.6000
The smallest decimal number is 0.4891.
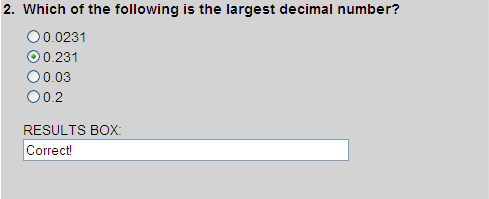
Writing one decimal beneath the other in their original order, we get:
0.0231
0.2310
0.0300
0.2000
Ordering these decimal from least to greatest, we get:
0.0231
0.0300
0.2000
0.2310
The largest decimal number is 0.231.
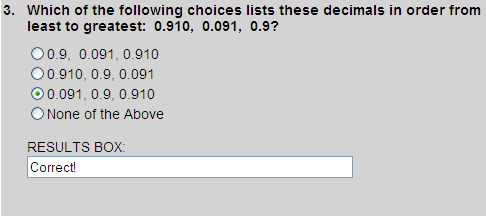
Writing one decimal beneath the other in their original order, we get:
0.910
0.091
0.900
Ordering these decimal from least to greatest, we get:
0.091
0.900
0.910
Thus, choice 3 is correct.
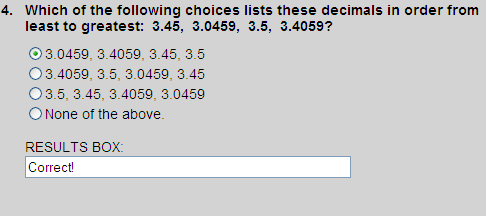
Writing one decimal beneath the other in their original order, we get:
3.4500
3.0459
3.5000
3.4059
Ordering these decimal from least to greatest, we get:
3.0459
3.4059
3.4500
3.5000
Thus, choice 1 is correct.
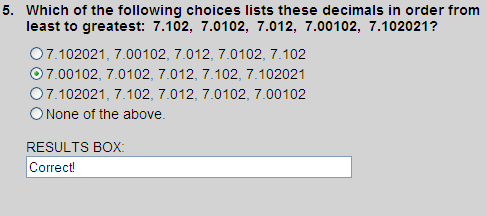
Writing one decimal beneath the other in their original order, we get:
7.102000
7.010200
7.012000
7.001020
7.102021
Ordering these decimal from least to greatest, we get:
7.001020
7.010200
7.012000
7.102000
7.102021
Thus, choice 2 is correct.
Estimating Decimal Sums
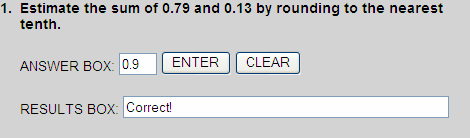
Rounding to the nearest tenth, we get:
0.79  0.8
0.8
0.13  0.1
0.1
0.8 + 0.1 = 0.9
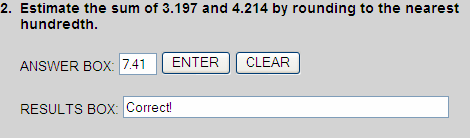
Rounding to the nearest hundredth, we get:
3.197  3.20
3.20
4.214  4.21
4.21
3.20 + 4.21 = 7.41
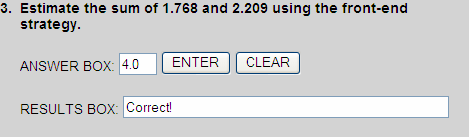
1 + 2 = 3
0.7 + 0.2 is almost equal to 1.0
3 + 1 = 4
4 = 4. = 4.0
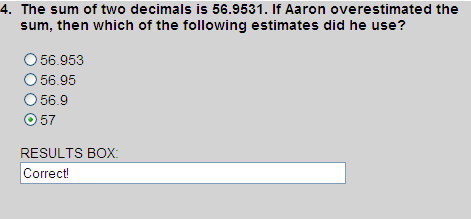
An overestimate is an an estimate that is too high: it exceeds the actual answer. The only estimate that is more than 56.9531 is 57. Thus choice 4 is correct.
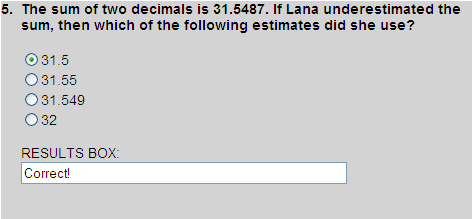
An underestimate is an estimate that is too low: it is lower than the actual answer. The only estimate that is less than 31.5487 is 31.5. Thus choice 1 is correct.
Adding Decimals
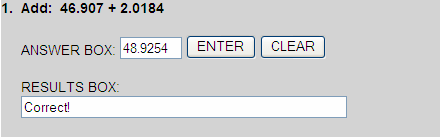
+ 46.9070
+ 2.0184
+ 48.9254
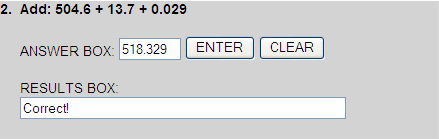
+ 504.600
+ 13.700
+ 0.029
+ 518.329
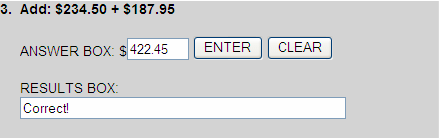
+ $234.50
+ $187.95
+ $422.45
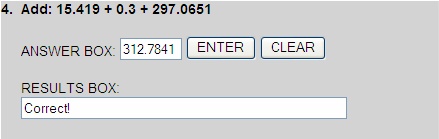
+ 15.4190
+ 0.3000
+ 297.0651
+ 312.7841
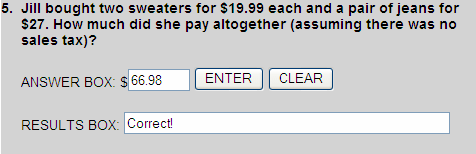
There were two sweaters.
+ $19.99
+ $19.99
+ $27.00
+ $66.98
Estimating Decimal Differences
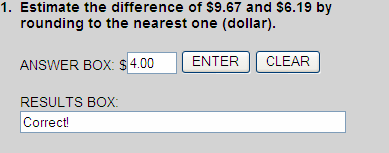
Rounding to the nearest one, we get:
$9.67 $10
$10
$6.19 $06
$06
- $10
- $ 6
- $ 4
Rounding to the nearest hundredth, we get:
2.995  3.00
3.00
1.997  2.00
2.00
- 3.00
- 2.00
- 1.00
Rounding to the nearest ten, we get:
63.7943  60
60
24.2581  20
20
- 60
- 20
- 40
An overestimate is an an estimate that is too high: it exceeds the actual answer. The only estimate that is more than 47.8943 is 48. Thus, choice 4 is correct.
Whether you round $15.98 to the nearest tenth, one or ten, you always get $16.00.
$50.00  $50.00
$50.00
$15.98  $16.00
$16.00
- $50.00
- $16.00
- $34.00
Thus, choice 2 is correct.
Subtracting Decimals
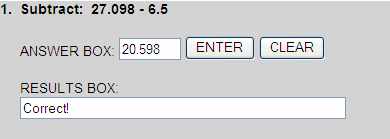
27.098
- 6.500
+ 20.598
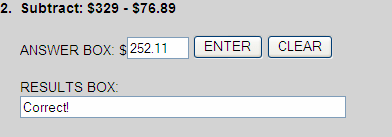
$329.00
- $ 76.89
+ $252.11
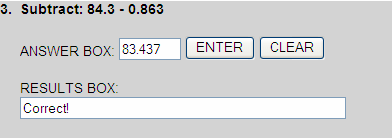
- 84.300
- 0.863
- 83.437
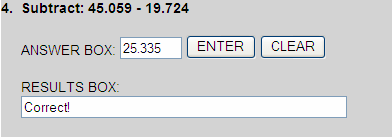
- 45.059
- 19.724
- 25.335
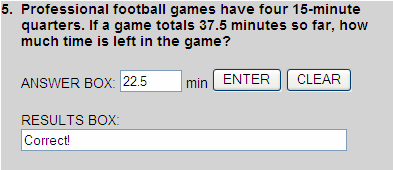
Four 15-minute quarters is 60 minutes.
- 60.0
- 37.5
- 22.5
Solving Decimal Word Problems
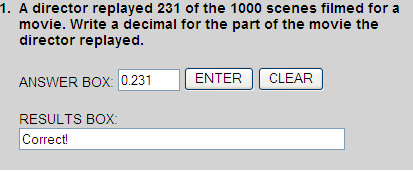
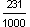 is shown in the place-value chart below.
is shown in the place-value chart below.
 |
 |
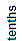 |
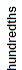 |
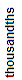 |
| 0 | . | 2 | 3 | 1 |
Ordering these decimals from least to greatest we get:
9.6, 9.625, 9.85
The winning time is the least of these decimals, 9.6 s.
+ 3.4375 cm
+ 0.0950 cm
+ 3.5325 cm
31.25  31
31
27.00  -27
-27
11.11 -14
Brandon must cut his time by about 4 s to reach his goal.
Deposits are added to, and withdrawals are subtracted from, a checking account.
+ $425.82
+ $120.75
+ $546.57
- $546.57
- $185.90
- $360.67
Practice Exercises
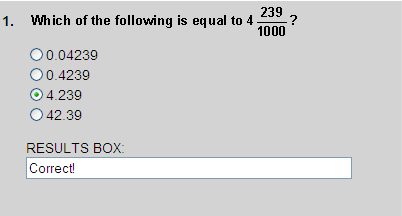
 is shown in the place-value chart below.
is shown in the place-value chart below.
 |
 |
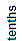 |
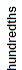 |
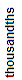 |
| 4 | . | 2 | 3 | 9 |
Nine hundred sixty-four and fifty-one hundredths is shown in the place-value chart below.
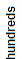 |
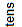 |
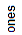 |
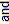 |
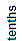 |
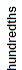 |
| 9 | 6 | 4 | . | 5 | 1 |
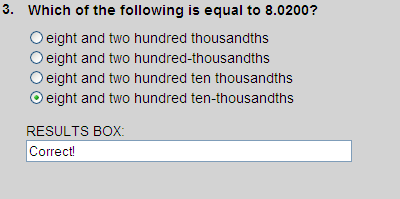
8.0200 is shown in the place-value chart below.
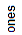 |
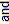 |
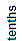 |
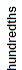 |
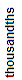 |
|
| 8 | . | 0 | 2 | 0 | 0 |
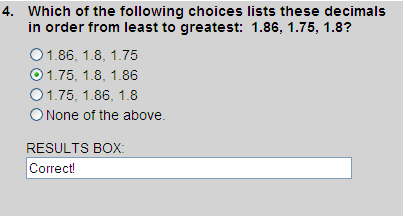
Writing one decimal beneath the other in their original order, we get:
1.86
1.75
1.80
Ordering these decimal from least to greatest, we get:
1.75
1.80
1.86
Thus, choice 2 is correct.
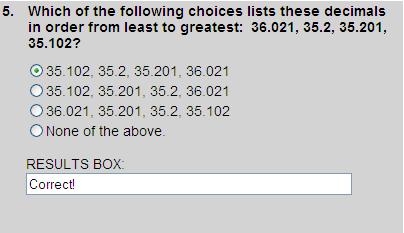
Writing one decimal beneath the other in their original order, we get:
36.021
35.200
35.201
35.102
Ordering these decimal from least to greatest, we get:
35.102
35.200
35.201
36.021
Thus, choice 1 is correct.
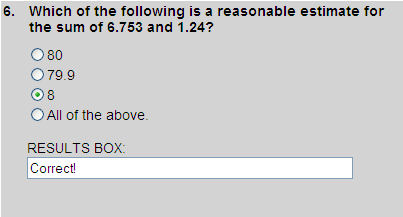
6.753  7
7
1.240  1
1
+ 7
+ 1
+ 8
Thus, choice 3 is correct. The estimates in choice 1 and choice 2 are unreasonable.
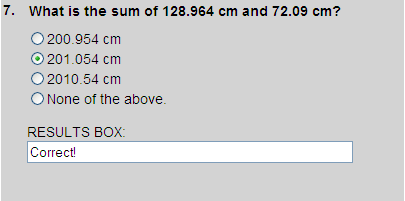
+ 128.964 cm
+ 72.090 cm
+ 201.054 cm
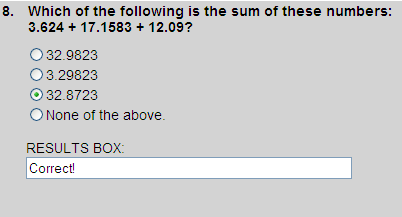
+ 3.6240
+ 17.1583
+ 12.0900
+ 32.8723
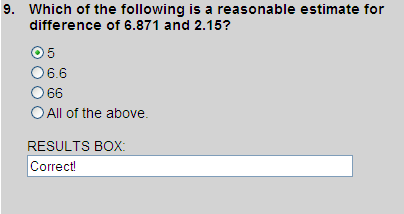
6.871  7
7
2.150  2
2
- 7
- 2
+ 5
Thus, choice 1 is correct. The estimates in choice 2 and choice 3 are unreasonable.
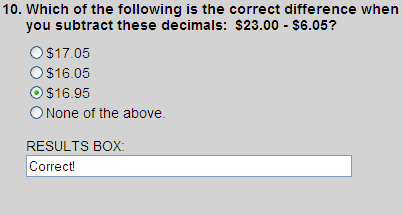
- $23.00
- $ 6.05
- $16.95
Thus, choice 3 is correct .
Challenge Exercises
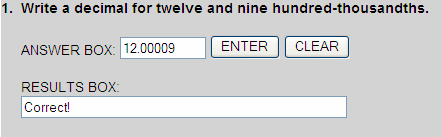
Twelve and nine hundred-thousandths is shown in the place-value chart below.
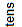 |
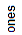 |
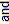 |
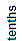 |
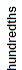 |
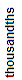 |
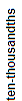 |
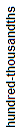 |
| 1 | 2 | . | 0 | 0 | 0 | 0 | 9 |
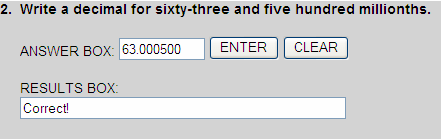
Sixty-three and five hundred millionths is shown in the place-value chart below.
 |
 |
 |
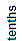 |
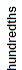 |
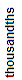 |
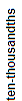 |
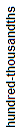 |
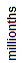 |
| 6 | 3 | . | 0 | 0 | 0 | 5 | 0 | 0 |
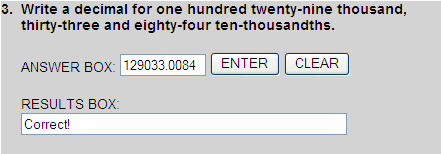
One hundred twenty-nine thousand, thirty-three and eighty-four ten-thousandths is shown in the place-value chart below.
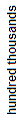 |
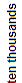 |
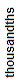 |
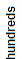 |
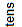 |
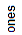 |
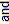 |
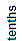 |
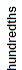 |
 |
 |
| 1 | 2 | 9 | 0 | 3 | 3 | . | 0 | 0 | 8 | 4 |
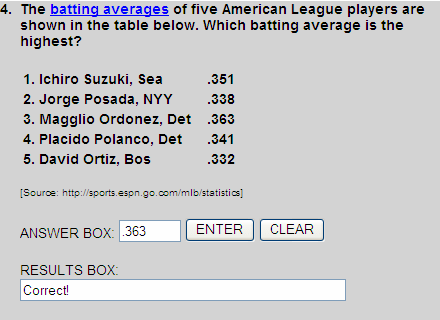
Ordering these decimal from least to greatest, we get:
0.332
0.338
0.341
0.351
0.363
Thus, the highest batting average is 0.363 (or .363).
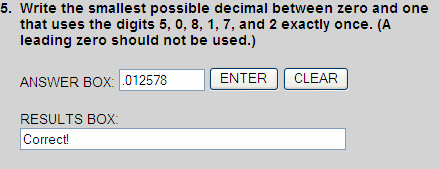
The smallest possible decimal between zero and one that uses the digits 5, 0, 8, 1, 7, and 2 exactly once is .012578. Use our Place Value Chart (PDF) for further assistance.
0 < .012578 < 1
The greatest possible decimal between zero and one that uses the digits 9, 0, 2, 6, 4 and 1 exactly once is 0.96421. The decimal 0.96421 can also be written as .964210. Use our Place Value Chart (PDF) for further assistance.
0 < 0.96421 < 1
Rounding to the nearest one, we get:
$978.50  + $ 979
+ $ 979
$489.95  + $ 490
+ $ 490
$162.79  + $ 163
+ $ 163
$076.12  + $ 76
+ $ 76
$076.12 + $1708
Adding the expenses from question 7, we get:
+ $ 978.50
+ $ 489.95
+ $ 162.79
+ $ 76.12
+ $1707.36
$50.00  - $50
- $50
$12.95  - $13
- $13
$50.00 - $37
$37 and $37.00 are equivalent decimals.
- 9.007
- 8.949
- 0.058
0.058 and .058 are equivalent decimals.




