Problem: The area of a rectangular garden is 24 square yards. List all possible whole-number dimensions the garden can have.
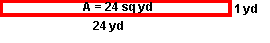
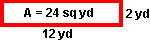
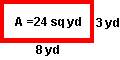
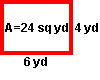
Solution: 1 yd x 24 yd, 2 yd x 12 yd, 3 yd x 8 yd, and 4 yd x 6 yd
The whole-number dimensions of this rectangular garden are the factors of the number 24. The following statements can be made about the factors of 24:
- The factors of 24 are: 1, 2, 3, 4, 6, 8, 12 and 24 since each of these numbers divides exactly into 24.
- The pairs of factors of 24 are: 1 and 24, 2 and 12, 3 and 8, and 4 and 6.
To find the factors of a whole number follow this procedure:
- Starting with 1, divide each counting number into the whole number.
- If the numbers divide exactly (no remainder), then you have found a pair of factors.
- List the counting number and the quotient of your division as a pair of factors.
- Keep dividing until a factor repeats.
- List all factors separated by commas.
Example 1: Find the factors of 12.
| Counting # | Division | Factor Pair |
|---|---|---|
| 1 | 12 ÷ 1 = 12 | 1 x 12 |
| 2 | 12 ÷ 2 = 6 | 2 x 6 |
| 3 | 12 ÷ 3 = 4 | 3 x 4 |
| 4 | 12 ÷ 4 = 3 | 4 x 3  |
Solution: The factors of 12 are 1, 2, 3, 4, 6 and 12.
(Note:  means that one or more factors has repeated so we stop dividing.)
means that one or more factors has repeated so we stop dividing.)
Example 2: Find the factors of 20.
| Counting # | Division | Factor Pair |
|---|---|---|
| 1 | 20 ÷ 1 = 20 | 1 x 20 |
| 2 | 20 ÷ 2 = 10 | 2 x 10 |
| 3 | 20 ÷ 3 = 6 R2 | -------- |
| 4 | 20 ÷ 4 = 5 | 4 x 5 |
| 5 | 20 ÷ 5 = 4 | 5 x 4  |
Solution: The factors of 20 are 1, 2, 4, 5, 10 and 20.
Example 3: Find the factors of 49.
| Counting # | Division | Factor Pair |
|---|---|---|
| 1 | 49 ÷ 1 = 49 | 1 x 49 |
| 2 | 49 ÷ 2 = 24 R1 | -------- |
| 3 | 49 ÷ 3 = 16 R1 | -------- |
| 4 | 49 ÷ 4 = 12 R1 | -------- |
| 5 | 49 ÷ 5 = 9 R4 | -------- |
| 6 | 49 ÷ 6 = 8 R1 | -------- |
| 7 | 49 ÷ 7 = 7 | 7 x 7  |
Solution: The factors of 49 are 1, 7 and 49
Problem: Find the Greatest Common Factor (GCF) of 12 and 20. (Note: Place your mouse over the lists of factors below.)
The common factors of 12 and 20 are 1, 2 and 4.
The greatest common factor of 12 and 20 is 4.
Solution: GCF = 4
To find the Greatest Common Factor (GCF) of two or more whole numbers, follow this procedure:
- Make a list of factors for each whole number.
- Identify all factors that are common to all lists.
- The Greatest Common Factor (GCF) is the largest of these common factors.
In Examples 4 through 6, place your mouse over the lists of factors to see the common factors.
Example 4: Find the GCF of 24 and 36.
The common factors of 24 and 36 are 1, 2, 3, 4, 6 and 12.
The greatest common factor of 24 and 36 is 12.
Solution: GCF = 12
Example 5: Find the GCF of 56 and 63.
The common factors of 56 and 63 are 1 and 7.
The greatest common factor of 56 and 63 is 7.
Solution: GCF = 7
Example 6: Find the GCF of 12, 30 and 54.
The common factors of 12, 30 and 54 are 1, 2, 3 and 6.
The greatest common factor of 12, 30 and 54 is 6.
Solution: GCF = 6
Summary: The factors of a whole number are those numbers that divide exactly into that whole number. The Greatest Common Factor (GCF) of a set of whole numbers is the largest factor common to all whole numbers in the set.
Exercises
Directions: Read each question below. Click once in an ANSWER BOX and type in your answer; then click ENTER. After you click ENTER, a message will appear in the RESULTS BOX to indicate whether your answer is correct or incorrect. To start over, click CLEAR.
| 1. | Find the GCF of 18 and 36. |
| 2. | Find the GCF of 30 and 48. |
| 3. | Find the GCF of 42 and 56. |
| 4. | Find the GCF of 16, 48 and 72. |
| 5. | One rectangular garden has an area of 18 square meters. Another rectangular garden has an area of 81 square meters. What is the largest possible whole-number dimension common to both gardens? |