What is Math Anxiety?
Tobias (1978) described it as "sudden death" (p. 46), but Kogelman and Warren (1979) say it is an adverse reaction to mathematics, while Byrd (1982) says it is any situation when one experiences anxiety "when confronted with mathematics in any way" (p. 38)
The developers of the MARS (Math Anxiety Rating Scale) say it "involves feelings of tension and anxiety that interfere with the manipulation of numbers and the solving of mathematical problems in a wide variety of ordinary and academic situations" Richardson and Suinn, 1972, p.551).
Why not other subject anxiety?
This may more particularly true of the study of mathematics because "mathematics offers what is perhaps the clearest and most concentrated example" of intelligent learning, "which is to say the formation of conceptual structures communicated and manipulated by means of symbols" (Skemp, 1971, p.16).
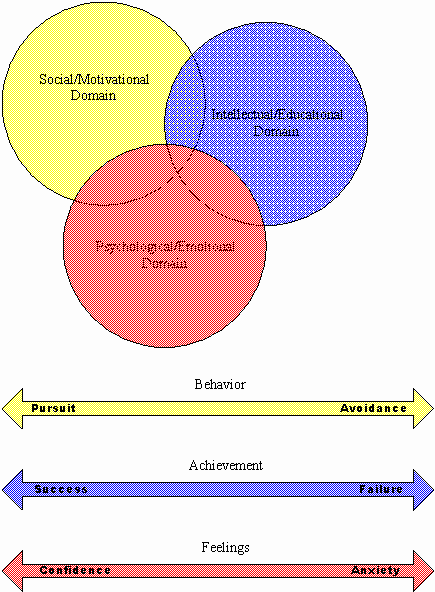
The Domains and Continua of the Model
There appear to be three major domains which are involved with the development of math anxiety. There is naturally some overlap between and among them and their boundaries are not well defined. In order to facilitate the development of this model of math anxiety, the domains will be treated as though they are distinct and well defined.
Associated with each domain is a continuum on which it is assumed that any student at any particular time may be found. The extremes of the continua are given and discussed below. The color codes associate each continuum with its appropriate Domain.
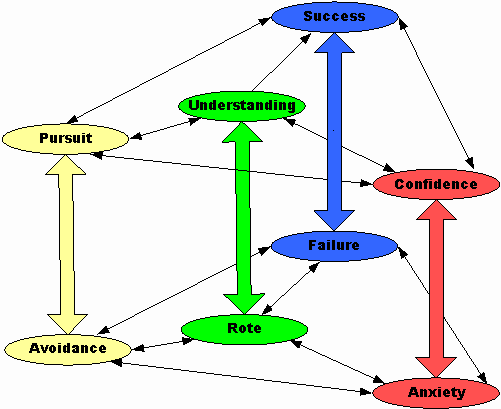
The Social / Motivational Domain includes those forces that act upon a person through the agencies of family, friends, and society as a whole. The continuum associated with this domain is Behavior because although choices are influenced by others, they are ultimately made by the individual. The Behavior Continuum has Pursuit and Avoidance as its opposites. These behaviors are logical consequences of the value place on mathematics, which is influenced by the attitudes of significant others and by society in general.
The Intellectual / Educational Domain is comprised of those influences that are cognitive in nature. Specifically, they include but are not limited to, the knowledge and skills an individual has and or is expected to acquire and his or her perception of success or failure in them. Although others may "grade" an individual’s performance in this domain, people form their own evaluations of their performance in this area. The continuum associated with this domain is Achievement, where individual perception is paramount. Success and Failure are the extremes of the Achievement Continuum, and are the subjective evaluation regarding one’s acquisition or use of mathematics skill and concepts.
The Psychological / Emotional Domain is formed by the faculties that are affective in nature. It is largely comprised of the individual’s emotional history, reactions to stimuli and arousal states. Hence the continuum associated with this domain is Feelings. At either end of the Feelings Continuum lie Anxiety and Confidence, although it could be argued that enjoyment is even further removed from anxiety than confidence. The assumption is that most students would find it puzzling to think of mathematics as enjoyable. Confidence can be equated with comfortableness, rather than pleasure.
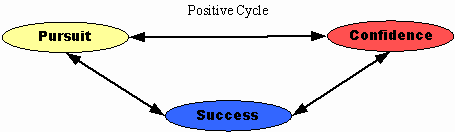
The extremes of the three continua comprise positive and negative cycles.
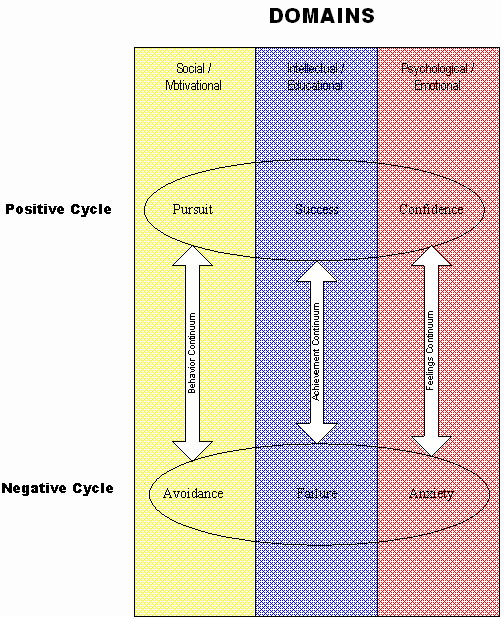
The three Domains are theorized to interact in a reinforcing fashion as illustrated by the cycles. In the following diagram.
In the Positive Cycle, an individual who is successful in the use and/or study of mathematics will be more confident in situation involving math and more likely to pursue the study or use of mathematics.

A similar relationship is theorized for both confidence and pursuit because a person who pursues the study of mathematics will tend to be more confident in math situations and will also tend to be more successful in its study and use. The latter is a logical assumption, for if one does not continue the study of mathematics, one cannot continue to be successful in learning it.

Research indicates that the more confidence a person has vis-à-vis mathematics, the more likely he or she is to be successful in such tasks (Betz, 1977, p.22), and the more confidence the individual has toward learning and using mathematics, the more likely he or she is to pursue its study.

The Negative Cycle operates in a similar way, with each component reinforcing the others. Failure in mathematics contributes is hypothesized to be an antecedent to math anxiety (Tobias & Weissbrod, 1980, p. 65). Since few people seek opportunities for failure, it is logical that avoiding mathematics would be a result of perceived or actual failure.

Anxiety reactions to mathematical situations may contribute to failure in mathematics (Tobias & Weissbrod, 1980, p.63). In fact, s person who has high math anxiety may actually be unable to perform well on test, and may be unable to learn in a mathematics classroom. Math anxiety also directly contributes to avoiding mathematics (Tobias & Weissbrod, 1980, p.63). It is logical to avoid situations which bring on anxiety reactions.

The ways in which avoidance contributes to failure and anxiety are perhaps a little less clear. Avoidance of mathematics engenders failure because a person who has successfully avoided mathematical situations for some time may lack the skills and knowledge needed when he or she is presented with a situation requiring its use. This is situation in which the individual is very likely to fail. Similarly, the person who has avoided mathematics and is suddenly confronted with a circumstance requiring it, is likely to be painfully aware of his or her lack of preparation and become anxious about it as a result. Thus the avoidance of mathematics can lead to failure and/or anxiety with staggering effect. Of course, if one could only continue to avoid mathematics situations, neither failure nor anxiety would result.

The phenomenon of math anxiety itself is of interest to the education community only because individuals find themselves placed in situation requiring that they either use or learn mathematics, or both. Without conditions necessitating the use of mathematics, math anxiety, however high the individual’s level, would not be of any consequence. An underlying assumption of this model is that math anxiety is of interest only to those people who have been influenced by it in the past, in career choices, for example, those who are influenced by it presently, as in a mathematics class, or those who will in influenced by it in the future, as in a required math class or job skill. As long as a perseon has no need for mathematics, math anxiety is unimportant.
The paths that people may travel in entering the Negative Cycle from the Positive Cycle may vary. This model was developed to illustrate the development of math anxiety, so the change from the Positive Cycle to the Negative Cycle will be our concern. Each Domain will be examined separately
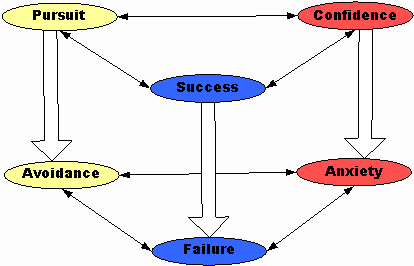
.In the Social / Motivational Domain movement along the Behavior Continuum from Pursuit to Avoidance can occur for many reasons. Sometimes it is a simple as students being extremely gifted in non-mathematical areas and choosing to spend their time and energy on the subject in which they are gifted. Individuals may also decide that the study or use of mathematics is not appropriate for them. This may be the result of sex-role stereotyping or other beliefs held by their socio-economic group.
The Intellectual / Educational Domain encompass the mostly academic influences on people. Many students move into the Negative Cycle through the Achievement Continuum when they no longer experience that they deem as success in the study of mathematics. Tobias asserted that "most people leave school as failures at math" (1978, p.26). Hilton (1980, p. 176) lists the causes of failure to be "bad teaching, bad texts, and bad educational instruments." He went on to include rote calculations, memory dependence, authoritarianism, spurious applications and unmotivated problems as additional factors which inhibit success in many students. Kogelman and Warren (1979) hypothesized that perceived rigidity of rules and an inordinate emphasis on right answers may drive some students, who are intellectually capable of learning mathematics from success to failure. In addition, the cumulative nature of mathematics may be a source of failure for students who must be absent from school for any length of time. Regardless of how or why individuals fail in mathematics, they often experience what Tobias (1978) calls "sudden death." Whether it was timed tests on multiplication facts, the introduction of operations fractions, multi-stage word problems, or solving equations that caused the difficulties, for many "failure was sudden and very frightening" (Tobias, 1978, p. 44). Presumably, students do not really just suddenly reach a concept or procedure that they cannot learn. In Lazarus’ (1974) analysis of math anxiety, he hypothesized a "latency stage" –a period in which the student has been relying on a memorize-what-to-do strategy in learning mathematics.
The Feelings Continuum is in the Psychological / Emotional Domain, with its extremes being Confidence and Anxiety. The transition from Confidence to Anxiety has been hypothesized to be the result of unpleasant experiences associated with learning or doing mathematics (Byrd, 1982; Kogelman & Warren, 1979; Tobias, 1978). Many people recall their first negative experiences with mathematics with surprising vividness and clarity. They may remember how the teacher looked or dressed and what type of mathematics task was involved. Students recollect mathematics being taught in an atmosphere of tension created by an emphasis on swift computations and correct answers (Tobias, 1978). Sometimes these negative experiences are not school related, but are associated with a parent or sibling who acts as tutor (Kogelman & Warren, 1979). In addition to these stresses, tests on mathematics serve as high stress producers. Kogelman & Warren (1979) found that mathematics "has long been associated with the pressures of performing and being evaluated" (p.58), and far too frequently, the associations are not pleasant ones. In short, movement from the Positive Cycle to the Negative Cycle can be precipitated by unpleasant emotions in a mathematics situation.
The model as presented thus far includes the influences that are chiefly affective in nature. What about cognitive variables? It is possible that they contribute strongly to the development of math anxiety. At the time this model was originally conceived and researched, there were no studies that directly addressed the role of cognition, specifically the role of understanding, with respect to the phenomenon called math anxiety. Cognition may be at the very heart of the matter.
In his foreword to Skemp’s The Psychology of Learning Mathematics, Foss stated that
mathematics is a curious subject, psychologically. It seems to divide people into two camps…there are those who can do mathematics and there are those who cannot, or who think they cannot, and who "block" at the first drop of a symbol. (cited in Skemp, 1971, p.9)
In fact, cognitive variables may have a greater impact than early research would indicate. Ashcraft and Kirk (2001) have been doing significant research in the area of how math anxiety may inhibit certain cognitive functions. They found that math anxiety may inhibit certain brain functions, possibly the very ones needed most for learning mathematics. So it is possible that math anxiety causes and is caused by failure to comprehend mathematics.
For the purposes of this model of math anxiety, however, learning will be examined with respect to its role in how people move between thePositive Cycle and the Negative Cycle. The Learning Continuum is hypothesized to have as its extremes Understanding and Rote Learning (listed as Rote).

That understanding and rote learning tend to be polar opposites in learning mathematics has long been understood. Carpenter et al., (1981) observed that students may concentrate on mastering rules to the extent of ignoring concomitant understanding, which means that they become totally dependent on mechanical algorithms, which are easily forgotten. "If students cannot remember a step in the algorithm, they cannot solve even simple problems that might be solved intuitively" (p.27). Learning by rote and learning with understanding are very different processes and have very different outcomes. There are important qualitative differences between students who have learned by rote and those who have learned with understanding (Simon, 1975; Skemp, 1971). Rote learners have difficulty applying learned skills in solving problems (Carpenter et al., 1981). In contrast, the "effects of understanding are cumulative; that is to say that "the greater the degree of understanding, the less the amount of practice necessary to promote and to fix learning" (Brownell, 1973, P.188), This may more particularly true of the study of mathematics because "mathematics offers what is perhaps the clearest and most concentrated example" of intelligent learning, "which is to say the formation of conceptual structures communicated and manipulated by means of symbols" (Skemp, 1971, p.16).
The following is a discussion of how the Learning Continuum fits with the other continua.
It is hypothesized that a mutually reinforcing relationship exists between understanding and the pursuit of mathematics learning. Students who understand the mathematics they are learning will be more likely to further pursue the subject. This may be because students who understand math may have a greater awareness of its usefulness and power, and pursue it for that reason. It may also be a result of the pleasure people experience from activities which are favorable to cognitive growth, which is "the most powerful incentive to leaning mathematics" (Skemp, 1971, p. 135). It is logical to assume that the pursuit of mathematics leads to understanding. Hartung (1953) asserted that increased motivation "may affect later learning experiences in ways which increase the level of achievement [understanding]" (p64).
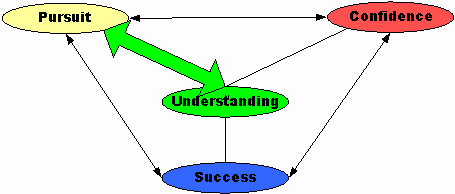
It also seems obvious that understanding mathematics enhances one’s success in the subject. The reverse direction: that success leads to understanding may be a logical assumption, but some educators assert that it is not at all the case. Skemp (1971) states that "learning to manipulate symbols in such a way as to obtain the approved answer may be very hard to distinguish, in its early stages, from conceptual learning" (p. 51). In fact, the leaner "cannot distinguish between the two if he has no experience of understanding mathematics" (Skemp, p. 51). Consequently the arrowhead from success to understanding is omitted in this model.
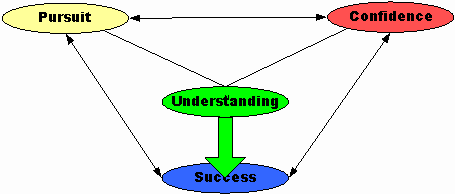
Understanding should increase students’ confidence in studying mathematics. Confidence in mathematics may lead to greater understanding, but confidence based on one’s ability to memorize, which yields apparently successful learning is fraught with peril. Confidence that arises from true understanding of mathematical concepts and processes, on the other hand, does engender further understanding. This becomes a sort of loop in which understanding builds confidence which, in turn, gives students increased assurance that they can learn new mathematical concepts, which raises confidence, etc.
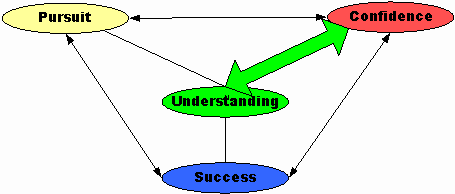
In the Negative Cycle just the reverse is true.
Rote learning often leads to avoidance
Visions of draconian teachers demanding insane memorization of meaningless mumbo-jumbo prevent a large number of people from reacting normally to the opportunities offered by contemporary mathematics. (Steen, 1978, p.2).
How avoidance of mathematics leads to rote learning is less obvious. If the student does not want to learn math, he or she may choose to just "try to learn what to do."
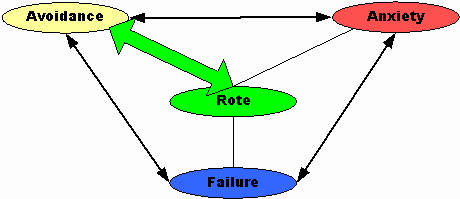
The relationship between rote learning and failure is obvious.
The amount which a bright child can memorize is remarkable, and the appearance of learning mathematics may be maintained until a level is reached at which only true conceptual learning is adequate to the situation. At this stage the learner tries to master the new tasks by the only means he knows--memorizing the rule for each kind of problem. This task being now impossible, even the outward appearance of progress ceases; and with accompanying distress, another pupil falls by the wayside. (Skemp, 1971, p.51)
Failure can lead to rote learning as the student attempts to master new material. Since he or she has experienced failure, perhaps the best thing is to try to "just learn what to do." Tobias (1978) described it as the penultimate solution.
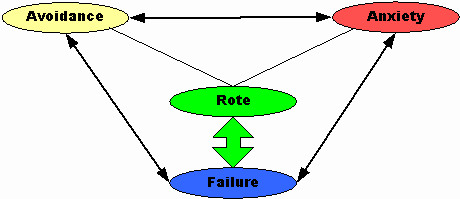
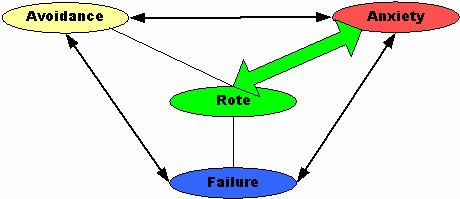
Skemp (1971) cites rote learning as in initial cause of mathematics anxiety (p.129). Memorization must eventually produce anxiety because first, as mathematics becomes more advanced the number of routines to memorized places a serious burden on the memory and second, a routine works only for a limited range of problems. Memorizing produces a short-term effect but not long-term retention, "so further progress comes to a standstill, with anxiety and loss of self-esteem" (Skemp, 1971. p.130).This becomes a double bind because since "higher mental activities are the first to be adversely affected by situation anxiety" (p.126-127), the only alternative is rote leaning. Skemp goes on to suggest that because rote learning is often faster, it may be favored because it brings "quicker relief from anxiety" (p.133).
So when we put it all together, the Model of Math Anxiety looks like this:
Math Anxiety Model
Affective and Cognitive
References
Ashcraft, M. & Kirk, E. P (2001, June) The relationships among working memory, math anxiety, and performance. Journal of Experimental Psychology: General, 130 (2), 24-237
Betz, N. E. (1978, September). Prevalence, distribution, and correlates of math anxiety in college students. Journal Of Counseling Psychology, 25(5), 441-448.
Brownell, W. A. (1973). Meaning and skill—Maintaining the balance. In F. J. Crosswhite, J. L. Higgins, A. R. Osborne, & R. J. Shumway (Eds.),Teaching mathematics: Psychological foundations (pp. 186-194). Worthington, OH: Jones Publishing.
Byrd, P.G (1982). A descriptive study of mathematics anxiety: Its nature and antecedents. Dissertation Abstracts International, 43, (8-A), 2583. (University Microfilms No. 8300843)
Carpenter, T. P., Corbitt, M. K., Kepner, H. S., Linquist, M. M., & Reyes, R. E. (1981). National assessment. In E. Fennema (Ed.), Mathematics educations research: Implications for the 80’s (pp. 22-40). Alexandria, VA: Association for Supervision and Curriculum Development.
Hartung, M. L. (1953). Motive for education in mathematics. In The Learning of Mathematics, 21st Yearbook (pp. 42-67). Washington, DC: National Council of Teachers of Mathematics.
Hilton, P.J. (1980). Math anxiety: Some suggested causes and cures, Part 2. Two-Year College Mathematics Journal, 11, 174-188.
Kogelman, S., & Warren, J. (1978). Mind over math. New York: McGraw-Hill.
Lazarus, M. (1974). Mathophobia: Some personal speculations. National Elementary Principal, 53 (2), 16-22.
Richardson, F.C., & Suinn, R.M. (1972, November). The mathematics anxiety rating scale: Psychometric data. Journal of Counseling Psychology,19 (6), 551-554.
Simon, H. A. (1975, March-April). Learning with understanding (Mathematics Education Report). Paper presented at the annual meeting of the American Education Association. (ERIC document Reproduction Service No. ED 113 206)
Skemp, R. (1971). The psychology of mathematics. Baltimore, MD: Penguin Books.
Steen, L.A.(Ed.). (1981). Mathematics tomorrow. New York: Springer-Verlag.
Tobias, S. (1978). Overcoming math anxiety. New York: Norton.
Tobias, S., 2& Weissbrod, C. (1980, February). Anxiety and mathematics: An update. Harvard Educational Review, 50(1), 63-70.
About The Author
Virginia W. Strawderman, Ph.D. did her dissertation on Math Anxiety. She has developed and produced the MathHELPS series of games and activities for young children.




