|
|
Converting Fractions
to
Mixed Numbers |
  |
Unit 14 > Lesson 7 of 11 |
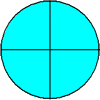
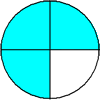
You may recall the example below from a previous lesson.
| Example 1 |
 |
|
|
|
|
|
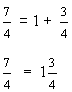In example 1, we used
circles to help us solve the problem. Now look at the next example.
|
| Example 2: |
At a birthday party, there are 19 cupcakes to be shared
equally among 11 guests. What part of the cupcakes will each guest get? |
  |
| Analysis: |
We need to divide 19 cupcakes by 11 equal parts. It would be
time-consuming to use circles or other shapes to help us solve this problem. Therefore, we
need an arithmetic method. |
| Step 1: |
Look at the fraction nineteen-elevenths below. Recall that the fraction bar means to divide
the numerator by the denominator. This is shown in step 2.
|
| Step 2: |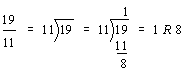
|
| Step 3: |
|
| Solution: |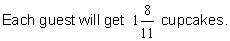
|
|
In example 2, the fraction nineteen-elevenths was converted to the mixed number one
and eight-elevenths. Recall that a mixed number consists of a whole-number
part and a fractional part. Let's look at some more examples of converting
fractions to mixed numbers using the arithmetic method.
|
| Example 3: |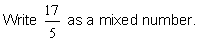
 |
| Analysis: |
We need to divide 17 into 5 equal parts |
| Step 1: |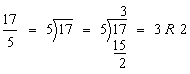
|
| Step 2: |
|
| Answer: |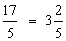
|
| Example 4: |
 |
| Analysis: |
We need to divide 37 into 10 equal parts. |
| Step 1: |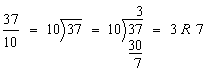
|
| Step 2: |
|
| Answer: |
|
| Example 5: |
 |
| Analysis: |
We need to divide 37 into 13 equal parts. |
| Step 1: |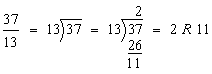
|
| Step 2: |
|
| Answer: |
|
| In each of the examples above, we converted a fraction to a mixed number through long division of
its numerator and denominator. Look at example 6 below. What is wrong with this problem?
|
| Example 6: |
 |
| Analysis: |
In the fraction seven-eighths, the numerator is less than
the denominator. Therefore, seven-eighths is a proper fraction less than 1. We
know from a previous lesson that a mixed number is greater than 1. |
| Answer: |
Seven-eighths cannot be written as a mixed number because it is a proper
fraction.
|
| Example 7: |
Can these fractions be written as mixed numbers? Explain
why or why not. |
|
 |
| Analysis: |
In each fraction above, the numerator is equal to the denominator.
Therefore, each of these fractions is an improper fraction equal
to 1. But a
mixed number is greater than 1. |
| Answer: |
These fractions cannot be written as mixed numbers since
each is an improper fraction equal to 1.
|
|
After reading examples 6 and 7, you may be wondering: Which types of fractions
can be written as mixed
numbers? To
answer this question, let's review an important chart from a previous lesson.
|
| Comparison of numerator and denominator |
Example |
Type of Fraction |
Write As |
| If the numerator < denominator, then the fraction < 1. |
 |
proper fraction |
proper fraction |
| If the numerator = denominator, then the fraction = 1. |
 |
improper fraction |
whole number |
| If the numerator > denominator, then the fraction > 1. |
 |
improper fraction |
mixed number |
|
The answer to the question is: Only an improper fraction greater than 1 can be
written to
a mixed number.
|
| Summary: |
We can convert an improper fraction greater than one to a mixed number through long division of
its numerator and denominator. |
Exercises
|
In Exercises 1 through 5, click once
in an ANSWER BOX and type in your answer; then click ENTER. After you click ENTER, a message will appear in the RESULTS BOX to
indicate whether your answer is correct or incorrect. To start over, click
CLEAR. Note: To write the mixed number four and two-thirds, enter 4, a
space, and then 2/3 into the form.
|
| 1. |
Write eleven-fifths as a mixed number.
|
|
|
|
|
| 2. |
Write eleven-fourths as a mixed number.
|
|
|
|
|
| 3. |
Write thirteen-ninths as a mixed number.
|
|
|
|
|
| 4. |
On field day, there are 23 pies to share equally among 7 classes. What
part of the pies will each class get?
|
|
|
|
|
| 5. |
A teacher gives her class a spelling test worth 35 points. If there are 8
words graded equally, then how many points is each word worth?
|
|
|
|
|
|
Interactive Math Goodies Software
