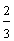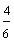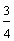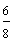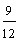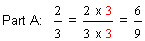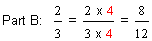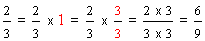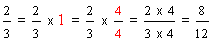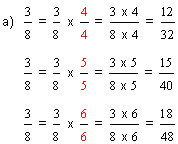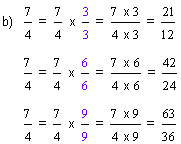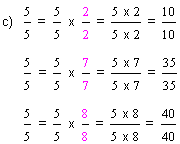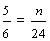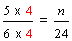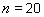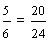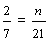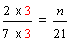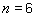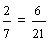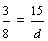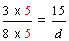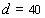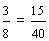Learn About Equivalent Fractions With Example Problems And Interactive Exercises.
Use the following examples and interactive exercises to learn about equivalent fractions.

What do the fractions in example 1 have in common?
Example 1

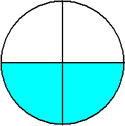
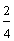
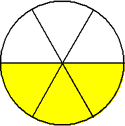
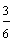
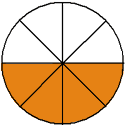
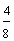
Each fraction in example 1 represents the same number. These are equivalent fractions.
Definition: Equivalent fractions are different fractions that name the same number.

Let's look at some more examples:
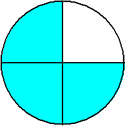
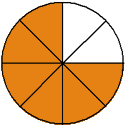
| Example 2 | ||||
|
||||
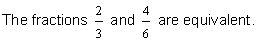 |
||||
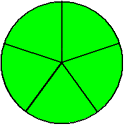
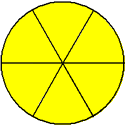
| Two-thirds is equivalent to four-sixths. |
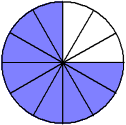
| Example 3 | ||||||||||
|
||||||||||
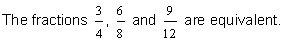 |
||||||||||
| The fractions three-fourths, six-eighths, and nine-twelfths are equivalent. |
What would happen if we did not have shapes such as circles and rectangles to refer to? Look at example 4 below.
Example 4
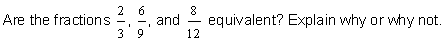
We need an arithmetic method for finding equal fractions.
Procedure:To find equivalent fractions, multiply the numerator AND denominator by the same nonzero whole number.
This procedure is used to solve example 4.
| Example 4 | ||
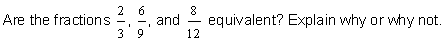 |
||
|
||
 |
You can multiply the numerator and the denominator of a fraction by any nonzero whole number, as long as you multiply both by the same whole number! For example, you can multiply the numerator and the denominator by 3, as shown in part A above. But you cannot multiply the numerator by 3 and the denominator by 5. You can multiply the numerator and the denominator by 4, as shown in part B above. But you cannot multiply the numerator by 4 and the denominator by 2.
The numerator and the denominator of a fraction must be multiplied by the same nonzero whole number in order to have equal fractions. You may be wondering why this is so. In the last lesson, we learned that a fraction that has the same numerator and denominator is equal to one. This is shown below.
2/2 = 1 (Two-halves)

3/3 = 1 (Three-thirds)
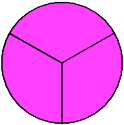
4/4 = 1 (Four-fourths)
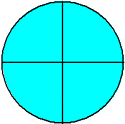
5/5 = 1 (Five-fifths)
6/6 = 1 (Six-sixths)
So, multiplying a fraction by one does not change its value. Recapping example 4, we get:
| Example 4 | ||
 |
||
|
||
 |
Multiplying the numerator and the denominator of a fraction by the same nonzero whole number will change that fraction into an equal fraction, but it will not change its value. Equal fractions may look different, but they have the same value, hence equal.
Let's look at some more examples:
| Example 5 |
 |
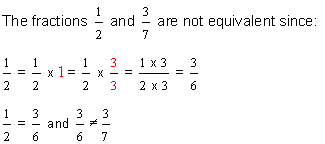 |
| Example 6 | ||
 |
||
|
|
||
In example 6, the fraction given in part a is a proper fraction; whereas the fractions given in parts b and c are improper fractions. Note that the procedure for finding equivalent fractions is the same for both types of fractions. Looking at each part of example 6, the answers vary, depending on the nonzero whole number chosen. However, the equivalent fractions found in each part all have the same value.
| Example 7 | ||||||||
| Write the fraction five-sixths as an equivalent fraction with a denominator of 24. | ||||||||
|
In example 7, we multiplied the numerator AND the denominator by 4.
| Example 8 | ||||||||
| Write the fraction two-sevenths as an equivalent fraction with a denominator of 21. | ||||||||
|
In example 8, we multiplied the numerator AND the denominator by 3.
| Example 9 | ||||||||
| Write the fraction three-eighths as an equivalent fraction with a numerator of 15. | ||||||||
|
In example 9, we multiplied the numerator AND the denominator by 5.
We can now redefine the terms fraction and equivalent fraction as follows:
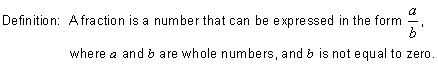
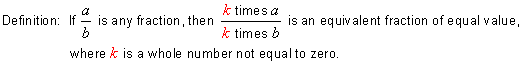
Summary: Equivalent fractions are different fractions that name the same number. The numerator and the denominator of a fraction must be multiplied by the same nonzero whole number in order to have equivalent fractions.
Exercises
In Exercises 1 through 5, click once in an ANSWER BOX and type in your answer; then click ENTER. After you click ENTER, a message will appear in the RESULTS BOX to indicate whether your answer is correct or incorrect. To start over, click CLEAR. Note: To write the fraction two-thirds, enter 2/3 into the form.
| 1. | Are the fractions three-fourths and fourteen-sixteenths equivalent (Yes or No)? |
| 2. | Write the fraction two-thirds as an equivalent fraction with a denominator of 18. (Enter the entire fraction into the form.) |
| 3. | Write the fraction eight-fifths as an equal fraction with a numerator of 40. (Enter the entire fraction into the form.) |
| 4. | Write the fraction seven-sevenths as an equivalent fraction with a denominator of 19. (Enter the entire fraction into the form.) |
| 5. | Write the fraction eleven-sevenths as an equal fraction with a denominator of 56. (Enter the entire fraction into the form.) |