Comparing Fractions - How to Find LCD

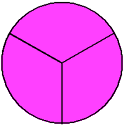
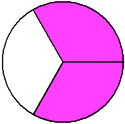
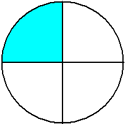
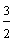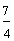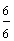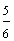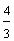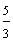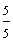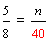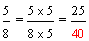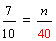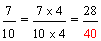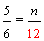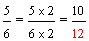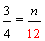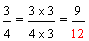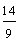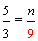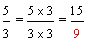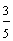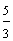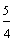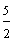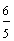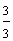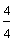Example 1: Drake rode his bike for three-fourths of a mile and Josh rode his bike for one-fourth of a mile. Which boy rode his bike farther?

Drake: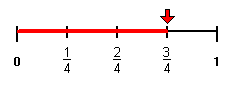 

Josh: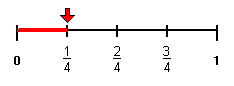 

Analysis:

?

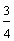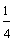These fractions have like denominators, so we can compare the numerators.

Solution:

>

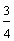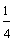Since three is greater than one, three-fourths is greater than one-fourth. Therefore, Drake rode his bike farther.

When comparing two fractions with like denominators, the larger fraction is the one with the greater numerator. Let's look at some more examples of comparing fractions with like denominators.

Example 2:  Compare the fractions given below using the symbols <, > or =. a)  ?     <  b)  ?     >  c)  ?     <  d)  ?     >  e)  ?     <  f)  ?     =

Example 3: Josephine ate three-fourths of a pie and Penelope ate two-thirds of a pie. If both pies are the same size, then which girl ate more pie?

Analysis:

?

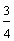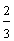These fractions have unlike denominators (and unlike numerators). It would be easier to compare them if they had like denominators. We need to convert these fractions to equivalent fractions with a common denominator in order to compare them more easily.

Josephine: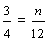  

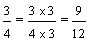
Penelope: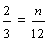  

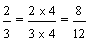
Solution: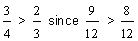 

Since nine-twelfths is greater than eight-twelfths, three-fourths is greater than two-thirds. Therefore, Josephine ate more pie.

The example above works out nicely! But how did we know to use 12 as our common denominator? It turns out that the least common denominator is the best choice for comparing fractions.

Definition: The least common denominator (LCD) of two or more non-zero denominators is the smallest whole number that is divisible by each of the denominators.

To find the least common denominator (LCD) of two fractions, find the least common multiple (LCM) of their denominators.

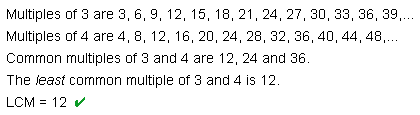
Remember that "..." at the end of each list of multiples indicates that the list goes on forever. Revisiting example 3, we found that the least common multiple of 3 and 4 is 12. Therefore, the least common denominator of two-thirds and three-fourths is 12. We then converted each fraction into an equivalent fraction with a denominator of 12, so that we could compare them.

Josephine: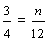  

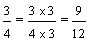
Penelope: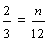  

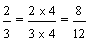
Procedure: To compare fractions with unlike denominators, follow these steps:

1. Use the LCD to write equivalent fractions with a common denominator.

2. Compare the numerators: The larger fraction is the one with the greater numerator.

Let's look at some more examples of comparing fractions with unlike denominators.

Example 4: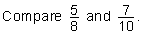
Analysis:	Convert these fractions to equivalent fractions with a common denominator in order to compare them.
Step1:	Find the least common multiple (LCM) of 8 and 10. multiples of 8 are 8, 16, 24, 32, 40, 48, 56, 64, 72, 80,... multiples of 10 are 10, 20, 30, 40, 50, 60, 70, 80,... The LCM of 8 and 10 is 40.
Analysis:
Step 2:	Convert each fraction to an equivalent fraction with a denominator of 40.
Answer: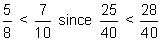

Example 5: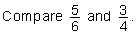
Analysis:	Convert these fractions to equivalent fractions with a common denominator in order to compare them.
Step 1:	Find the least common multiple (LCM) of 6 and 4. multiples of 6 are 6, 12, 18, 24, 30, 36,... multiples of 4 are 4, 8, 12, 16, 20, 24, 28, 32, 36,... The LCM of 6 and 4 is 12.
Analysis:
Step 2:	Convert each fraction to an equivalent fraction with a denominator of 12.
Answer: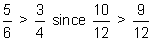

Example 6: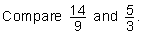
Analysis:	Convert these fractions to equivalent fractions with a common denominator in order to compare them.
Step 1:	Find the least common multiple (LCM) of 9 and 3. multiples of 9 are 9, 18, 27, 36, 45, 54, 63, 72,... multiples of 3 are 3, 6, 9, 12, 18, 21, 24, 27, 30, 33, 36,... The LCM of 9 and 3 is 9.
Analysis:
Step 2:	Convert each fraction to an equivalent fraction with a denominator of 9.
Answer: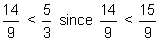

In this lesson, we have compared fractions with like denominators and with unlike denominators. Let's see what happens when we compare fractions with like numerators. Look at the shaded rectangles below.

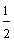
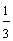
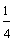
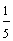
The fractions above all have the same numerator. (Each of these fractions is called a unit fraction.) As the denominator gets larger, the fraction gets smaller. To compare fractions with like numerators, look at the denominators. The fraction with the smaller denominator is the larger fraction. Let's look at some examples.

>

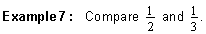Since one-half has the smaller denominator, it is the larger fraction.

<

Since three-fourths has the smaller denominator, it is the larger fraction.

5/3 (five-thirds) 5/4 (Five-fourths)

>

Since five-thirds has the smaller denominator, it is the larger fraction. Remember, when comparing fractions with like numerators, the fraction with the smaller denominator is the larger fraction. Let's look at some more examples of comparing fractions with like numerators.

Example 10:  Compare the fractions given below using the symbols <, > or =. a)  ?     <  b)  ?     >  c)  ?     <  d)  ?     >  e)  ?     <

3/3 (Three-thirds)	4/4 (Four-fourths)
=

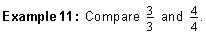Note that the improper fractions in example 11 are equivalent. This is because for each fraction, the numerator is equal to its denominator. So, each fraction is equivalent to 1. We have looked at many examples in this lesson. Let's try to summarize what we have learned.

R U L E S  F O R  C O M P A R I N G  F R A C T I O N S

Relationship: Like Denominators

How To Compare: Look at the numerators. The larger fraction is the one with the greater numerator.

Example: 

>

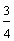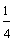Relationship: Unlike Denominators

How To Compare: Convert each fraction to an equivalent fraction with a common denominator. The larger fraction is the one with the greater numerator.

​Example: 

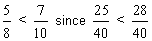
Relationship: Like Numerators

How To Compare: Look at the denominators. The fraction with the smaller denominator is the larger fraction.

​Example:

>

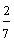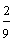Summary: In this lesson, we learned how to compare fractions with like denominators, with unlike denominators, and with like numerators. To compare fractions with unlike denominators, use the LCD to write equivalent fractions with a common denominator; then compare the numerators.

Exercises

In Exercises 1 through 5, click once in an ANSWER BOX and type in your answer; then click ENTER. After you click ENTER, a message will appear in the RESULTS BOX to indicate whether your answer is correct or incorrect. To start over, click CLEAR. Note: To write the fraction two-thirds, enter 2/3 into the form.