Problem: Two students multiplied 0.2 by 0.4. Student 1 found a product of 0.8 and Student 2 found a product of 0.08. Which student had the correct answer? Explain.
| Student 1 | Student 2 | |
Analysis: Let's convert each decimal to a fraction to help us solve this problem.
| Factors | Product | ||||
| Fractions: | x |
|
= |
|
|
| Decimals: | 0.2 | x | 0.4 | = | 0.08 |
If we multiply two tenths by four tenths, we get a product of eight hundredths.
Answer: Student 2 is correct since 0.2 x 0.4 = 0.08.
In the problem above, the product 0.08 is smaller than each individual factor. This is because you are finding a part of a part: 0.2 of 0.4 is 0.08. Thus, when you multiply two decimal factors, where each is less than one, the product will be less than each individual factor. Let's look at some more examples of multiplying decimals.
 Example 1: Marina's car gets 44.8 miles per gallon on the highway. If her fuel tank holds 15.4 gallons, then how far can she travel on one full tank of gas?
Example 1: Marina's car gets 44.8 miles per gallon on the highway. If her fuel tank holds 15.4 gallons, then how far can she travel on one full tank of gas?
Analysis: We can multiply 44.8 by 15.4 to solve this problem.
Step 1: Estimate the product.
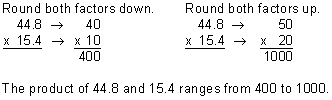
Step 2: Multiply to find the product.
Multiply these decimals as if they were whole numbers. Ignore the decimal point.
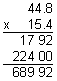
Compensate by placing the decimal point in the product.
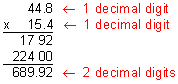
Step 3: Compare your estimate with your product to verify that your answer makes sense.
Our answer of 689.92 makes sense since the product of 44.8 and 15.4 ranges from 400 to 1,000.
Answer: Marina can travel 689.92 miles with one full tank of gas.
When multiplying decimals, placement of the decimal point is very important. Since there is one decimal digit in each factor, there must be two decimal digits in the product. This is because tenths x tenths = hundredths. Estimating the product lets us verify that the placement of the decimal point is correct, and that we have a reasonable answer. For example, if your product was 68.992 miles, then you would know that you made a multiplication error after comparing it with your estimate. Let's look at some more examples of multiplying decimals.
Example 2: Multiply: 3.54 x 1.8
Analysis: There are two decimal digits in the factor 3.54 and 1 decimal digit in the factor 1.8.
Step 1: Estimate the product.
![]()
Step 2: Multiply to find the product.
Multiply these decimals as if they were whole numbers. Ignore the decimal point.
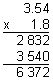
Compensate by placing the decimal point in the product.
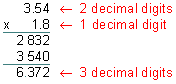
Step 3: Compare your estimate with your product to verify that your answer makes sense.
Our product of 6.372 makes sense since it is close to our estimate of 6.
Answer: The product of 3.54 and 1.8 is 6.372
In Example 2, there are two decimal digits in the factor 3.54 and one decimal digit in the factor 1.8. Therefore, there must be three decimal digits in the product. Perhaps you are wondering why this is so. When we ignored the decimal point in Step 2, we really moved it two places to the right for the first factor (3.54 x 100 = 354.) and one place to the right for the second factor (1.8 x 10 = 18.). We need to compensate to get the right answer. To do this, we must add up the total number of places the decimal point was moved to the right. Then, starting from the right of the last digit in the product, we must move the decimal point the same number of places to the left. In short, since we multiplied by 10 to the third power, we must compensate by dividing by 10 to the third power. Let's look at another example.
Example 3: Multiply: 0.121 x 0.02
Analysis: There are three decimal digits in the factor 0.121 and 2 decimal digits in the factor 0.02.
Step 1: Estimate the product.
![]()
Step 2: Multiply to find the product.
Multiply these decimals as if they were whole numbers. Ignore the decimal point.
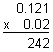
Compensate by placing the decimal point in the product.
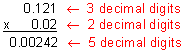
Step 3: Compare your estimate with your product to verify that your answer makes sense.
Our product of 0.00242 makes sense since it is close to our estimate of 0.00240
Answer: The product of 0.121 and 0.02 is 0.00242.
In Example 3, there are three decimal digits in the factor 0.121 and two decimal digits in the factor 0.02. Therefore, there must be five decimal digits in the product. When we ignored the decimal point in Step 2, we really moved it three places to the right for the first factor (0.121 x 1,000 = 121.) and two places to the right for the second factor (0.02 x 100 = 2.). We need to compensate to get the right answer. To do this, we must add up the total number of places the decimal point was moved to the right. Then, starting from the right of the last digit in the product, we must move the decimal point five places to the left. The product 242 only has 3 digits in it. Thus, we need to write two zeros to the left of it so there would be enough places to move the decimal point. In short, since we multiplied by 10 to the fifth power, we must compensate by dividing by 10 to the fifth power. Let's look at another example.
Example 4: Multiply: 5.27 x 0.01
Analysis: There are two decimal digits in each factor.
Step 1: Estimate the product.
![]()
Step 2: Multiply to find the product.
Multiply these decimals as if they were whole numbers. Ignore the decimal point.
![]()
Compensate by placing the decimal point in the product.
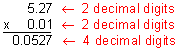
Step 3: Compare your estimate with your product to verify that your answer makes sense
Our product of 0.0527 makes sense since it is close to our estimate of 0.05.
Answer: The product of 5.27 and 0.01 is 0.0527.
Note that in Example 4, there are two decimal digits in each factor, which resulted in four decimal digits in the product. The product 527 only has 3 digits in it. Thus, we need to write one zero to the left of it so there would be enough places to move the decimal point. Let's look at some more examples.
Example 5: Multiply: 2.1 x 8.9
Analysis: There are two decimal digits in each factor.
Step 1: Estimate the product.
Can you estimate the product using mental arithmetic?
Step 2: Multiply to find the product.
Multiply these decimals as if they were whole numbers. Ignore the decimal point.
![]()
Compensate by placing the decimal point in the product.

Step 3: Compare your estimate with your product to verify that your answer makes sense
Our product of 18.69 makes sense since it is close to our mental estimate of 18.
Answer: The product of 2.1 and 8.9 is 18.69.
Note that in Example 5, there is one decimal digit in each factor, which resulted in two decimal digits in the product. Let's look at one more example.
 Example 6: Sam studied for 3.5 hours every day for 4.5 days. How many hours did he study?
Example 6: Sam studied for 3.5 hours every day for 4.5 days. How many hours did he study?
Analysis: We will multiply to solve this problem.
![]()
![]()
Answer: Sam studied for 15.75 hours.
Summary: When multiplying decimals, we use the following procedure:
- Estimate the product.
- Multiply to find the product.
- Multiply the decimals as if they were whole numbers. Ignore the decimal point.
- Compensate by placing the decimal point in the product.
- Compare your estimate with your product to verify that your answer makes sense.
Estimating the product before we multiply lets us verify that the placement of the decimal point is correct, and that we have a reasonable answer. When we ignore the decimal point, we have really moved it to the right of each factor. Since we multiplied each factor by a power of 10, we need to compensate to get the right answer. To do this, we must add up the total number of places the decimal point was moved to the right. Then, starting from the right of the last digit in the product, we must move the decimal point the same number of places to the left.
Exercises
Directions: Read each question below. You may use paper and pencil to help you multiply. Click once in an ANSWER BOX and type in your answer; then click ENTER. After you click ENTER, a message will appear in the RESULTS BOX to indicate whether your answer is correct or incorrect. To start over, click CLEAR.
| 1. |
Multiply: 0.7 x 0.6 |
| 2. |
Multiply: $3.05 x 0.8 |
| 3. |
Multiply: 0.46 x 8.61 |
| 4. |
Multiply: 9.7 x 0.001 |
| 5. |
A tutor earns $41.50 per hour. How much will he earn if he works for 3.25 hours (rounded to the nearest cent)? |




