Learn About Decimals and Decimals Place Value With The Following Examples And Interactive Exercises
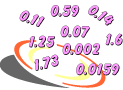
Problem: Order these numbers from least to greatest:
![]()
Analysis: We know that ![]() is a mixed number: it consists of a whole number and a fraction. Let's use place value to help us compare these numbers
is a mixed number: it consists of a whole number and a fraction. Let's use place value to help us compare these numbers
57= (5 x 10) + (7 x 1)
![]() = (5 x 10) + ( 7 x 1) + (4 x
= (5 x 10) + ( 7 x 1) + (4 x ![]() ) + (9 x
) + (9 x ![]() )
)
58= (5 x 10) + (8 x 1)
Answer: Ordering these numbers from least to greatest, we get:
![]()
That's a lot of writing! We can use decimals to write ![]() more easily.
more easily.
Definition: A decimal is any number in our base-ten number system. Specifically, we will be using numbers that have one or more digits to the right of the decimal point in this unit of lessons. The decimal point is used to separate the ones place from the tenths place in decimals. (It is also used to separate dollars from cents in money.) As we move to the right of the decimal point, each number place is divided by 10.
Below we have expressed the number ![]() in expanded form and in decimal form.
in expanded form and in decimal form.
| Mixed Number | - Expanded Form - | Decimal Form | |
| = (5 x 10) + ( 7 x 1) | + (4 x |
= 57.49 | |
As you can see, it is easier to write ![]() in decimal form. Let's look at this decimal number in a place-value chart to better understand how decimals work.
in decimal form. Let's look at this decimal number in a place-value chart to better understand how decimals work.
| PLACE VALUE AND DECIMALS | |||||||||||||
| |
|
|
|
||||||||||
| 5 | 7 | . | 4 | 9 | |||||||||
As we move to the right in the place value chart, each number place is divided by 10. For example, thousands divided by 10 gives you hundreds. This is also true for digits to the right of the decimal point. For example, tenths divided by 10 gives you hundredths. When reading decimals, the decimal point should be read as "and." Thus, we read the decimal 57.49 as "fifty-seven and forty-nine hundredths." Note that in daily life it is common to read the decimal point as "point" instead of "and." Thus, 57.49 would be read as "fifty-seven point four nine." This usage is not considered mathematically correct.
Example 1: Write each phrase as a fraction and as a decimal.
| phrase | fraction | decimal |
| six tenths | .6 | |
| five hundredths | .05 | |
| thirty-two hundredths | .32 | |
| two hundred sixty-seven thousandths | .267 |
So why do we use decimals?
Decimals are used in situations which require more precision than whole numbers can provide. A good example of this is money: Three and one-fourth dollars is an amount between 3 dollars and 4 dollars. We use decimals to write this amount as $3.25.
A decimal may have both a whole-number part and a fractional part. The whole-number part of a decimal are those digits to the left of the decimal point. The fractional part of a decimal is represented by the digits to the right of the decimal point. The decimal point is used to separate these parts. Let's look at some examples of this.
| decimal | whole-number part | fractional part |
| 3.25 | 3 | 25 |
| 4.172 | 4 | 172 |
| 25.03 | 25 | 03 |
| 0.168 | 0 | 168 |
| 132.7 | 132 | 7 |
Let's examine these decimals in our place-value chart.
| PLACE VALUE AND DECIMALS | |||||||||||||
| |
|
|
|
||||||||||
| 3 | . | 2 | 5 | ||||||||||
| 4 | . | 1 | 7 | 2 | |||||||||
| 2 | 5 | . | 0 | 3 | |||||||||
| 0 | . | 1 | 6 | 8 | |||||||||
| 1 | 3 | 2 | . | 7 | |||||||||
Note that 0.168 has the same value as .168. However, the zero in the ones place helps us remember that 0.168 is a number less than one. From this point on, when writing a decimal that is less than one, we will always include a zero in the ones place. Let's look at some more examples of decimals.
Example 2: Write each phrase as a decimal.
| Phrase | Decimal |
| fifty-six hundredths | 0.560 |
| nine tenths | 0.900 |
| thirteen and four hundredths | 13.040 |
| twenty-five and eighty-one hundredths | 25.810 |
| nineteen and seventy-eight thousandths | 19.078 |
Example 3: Write each decimal using words.
| Decimal | Phrase |
| 0.0050 | five thousandths |
| 100.6000 | one hundred and six tenths |
| 2.2800 | two and twenty-eight hundredths |
| 71.0620 | seventy-one and sixty-two thousandths |
| 3.0589 | three and five hundred eighty-nine ten-thousandths |
Expanded Form
We can write the whole number 159 in expanded form as follows: 159 = (1 x 100) + (5 x 10) + (9 x 1). Decimals can also be written in expanded form. Expanded form is a way to write numbers by showing the value of each digit. This is shown in the example below.
Example 4: Write each decimal in expanded form.
| Decimal | Expanded form | |
| 4.1200 | = | (4 x 1) + (1 x |
| 0.9000 | = | (0 x 1) + (9 x |
| 9.7350 | = | (9 x 1) + (7 x |
| 1.0827 | = | (1 x 1) + (0 x |
Decimal Digits
In the decimal number 1.0827, the digits 0, 8, 2 and 7 are called decimal digits.
Definition: In a decimal number, the digits to the right of the decimal point that name the fractional part of that number, are called decimal digits.
Example 5: Identify the decimal digits in each decimal number below.
| Decimal Number | Decimal Digits |
| 1.40000 | 1.40000 |
| 359.62000 | 359.62000 |
| 54.00170 | 54.00170 |
| 0.72900 | 0.72900 |
| 63.10148 | 63.10148 |
Writing whole numbers as decimals
A decimal is any number, including whole numbers, in our base-ten number system. The decimal point is usually not written in whole numbers, but it is implied. For example, the whole number 4 is equivalent to the decimals 4. and 4.0. The whole number 326 is equivalent to the decimals 326. and 326.0. This important concept will be used throughout this unit.
Example 6: Write each whole number as a decimal.
| Whole Number | Decimal | Decimal with 0 |
| 17 | 17. | 17.0 |
| 459 | 459. | 459.0 |
| 8 | 8. | 8.0 |
| 1,024 | 1,024. | 1,024.0 |
| 519 | 519. | 519.0 |
| 63,836 | 63,836. | 63,836.0 |
Often, extra zeros are written to the right of the last digit of a decimal number. These extra zeros are place holders and do not change the value of the decimal. For example:
| 7.5 = | 7.50 = | 7.500 = | 7.5000 | and so on. |
| 9 = | 9. = | 9.0 = | 9.00 | and so on. |
Note that the decimals listed above are equivalent decimals.
So how long can a decimal get?
A decimal can have any number of decimal places to the right of the decimal point. An example of a decimal number with many decimal places is the numerical value of Pi, shortened to 50 decimal digits, as shown below:
3.14159 26535 89793 23846 26433 83279 50288 41971 69399 37510
Summary: A decimal is any number in our base ten number system. In this lesson we used numbers that have one or more digits to the right of the decimal point. The decimal point is used to separate the whole number part from the fractional part; it is handy separator. Decimal numbers are used in situations which require more precision than whole numbers can provide. As we move to the right of the decimal point, each number place is divided by 10.
Exercises
Directions: Read each question below. Select your answer by clicking on its button. Feedback to your answer is provided in the RESULTS BOX. If you make a mistake, choose a different button.
| 1. | Which of the following is equal to |
| 2. | Which of the following is equal to |
| 3. | Which decimal represents seven hundred sixty-two and three tenths? |
| 4. | Which of the following is the expanded form of 0.546? |
| 5. | Which of the following is equal to twenty-five and sixty-nine thousandths? |




