 Example 1: Polygon Pizza Place caters children's parties with square-shaped pizza. Each pizza is exactly the same size and is divided into equal parts called slices. At Sam's party, each child had 2 out of 10 slices from a single pizza. At Elena's party, each child had 15 out of 100 slices from a single pizza. At which party did each child have more pizza?
Example 1: Polygon Pizza Place caters children's parties with square-shaped pizza. Each pizza is exactly the same size and is divided into equal parts called slices. At Sam's party, each child had 2 out of 10 slices from a single pizza. At Elena's party, each child had 15 out of 100 slices from a single pizza. At which party did each child have more pizza?
Analysis: We can write a fraction to represent each party:
| Party |
Fraction |
| Sam's |
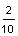 |
| Elena's |
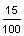 |
|
|
Using our knowledge of decimals, we get:
| Party |
Fraction |
Decimal |
| Sam's |
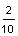 |
0.2X |
| Elena's |
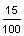 |
0.15 |
|
|
Answer: Each child got more pizza at Sam's Party.
In Example 1, we compared two decimal numbers and found that 0.2 is greater than 0.15. Some students would argue that 0.15 is a longer decimal with more digits, and is therefore greater than 0.2. However, if we think about money, we know that 20 cents is greater than 15 cents. Thus, our answer in Example 1 is correct.
Decimal numbers are compared in the same way as other numbers: by comparing the different place values from left to right. We use the symbols <, > and = to compare decimals as shown below.
| Comparison |
Meaning |
| 0.2 > 0.15 |
0.2 is greater than 0.15 |
| 0.15 < 0.2 |
0.15 is less than 0.2 |
| 0.2 = 0.2 |
0.2 is equal to 0.2 |
| 0.15 = 0.15 |
0.15 is equal to 0.15 |
When comparing two decimals, it is helpful to write one below the other. This is shown in the next example.
Example 2; Which is greater, 0.57 or 0.549?
Analysis: Let's compare these decimals using a place-value chart.
Answer: 0.57 is greater than 0.549.
Notation: 0.57 > 0.549
As you can see in the example above, 0.57 has fewer decimal digits than 0.549. It is easier to compare two decimals when you have the same number of decimal digits, so an extra zero was written to the right of the digit 7 in the decimal 0.57. We are able to do this because 0.57 and 0.570 are equivalent decimals.
Use Caution With Writing Extra Zeros
It is easier to compare decimals when you have the same number of decimal digits. Thus, we often write extra zeros to the right of the last digit of one of the decimals being compared. These extra zeros are place holders and do not change the value of the decimal. However, if you inserted a zero between the decimal point and a decimal digit, thatwould change the value of the decimal. This is shown in the table below:
0.57=0.570=0.5700 - Writing extra zeros to the right of the last digit of a decimal does not change its value.
0.57≠0.507≠0.057 = Inserting a zero between the decimal point and a decimal digit does change the value of a decimal.
Let's look at some more examples of comparing decimals.
Example 3: Compare each pair of decimals using the symbols <, > or =.
Example 4: Compare each pair of decimals using the symbols <, > or =.
In Examples 3 and 4, there were some problems in which the two decimals being compared did not have the same number of decimal digits. In these problems, we wrote one or more extra zeros to the right of the last digit of one decimal so that both decimals would have the same number of decimal digits. In the examples above, we used place-value charts to help us compare decimals. Let's try some examples without place-value charts.
Example 5: Compare each pair of decimals using the symbols <, > or =.
| 0.1379 |
|
0.01379 |
| 2.4896 |
|
2.4986 |
| 7.914 |
|
791.4 |
| $2.39 |
|
2.39 |
| 0.81734 |
|
0.08174 |
| Problem |
|
Answer |
|
| 0.13790 |
|
0.1379 |
> |
0.01379 |
| 0.01379 |
|
|
| 2.4896 |
|
2.4896 |
< |
2.4986 |
| 2.4986 |
|
|
| 7.914 |
|
7.914 |
< |
791.4 |
| 791.400 |
|
|
| $2.39 |
|
$2.39 |
= |
2.39 |
| 2.39 |
|
|
| 0.81734 |
|
0.81734 |
> |
0.08174 |
| 0.08174 |
|
|
Example 6: Compare each pair of decimals using the symbols <, > or =.
| 1.46197 |
|
1.046197 |
| 15.317965 |
|
15.317965 |
| 4.7293 |
|
4.7923 |
| 0.78154 |
|
0.78514 |
| $0.96 |
|
$0.91 |
| Problem |
|
Answer |
|
| 1.461970 |
|
1.46197 |
> |
1.046197 |
| 1.046197 |
|
|
| 15.317965 |
|
15.317965 |
= |
15.317965 |
| 15.317965 |
|
|
| 4.7293 |
|
4.7293 |
< |
4.7923 |
| 4.7923 |
|
|
| 0.78154 |
|
0.78154 |
< |
0.78514 |
| 0.78514 |
|
|
| $0.96 |
|
$0.96 |
> |
$0.91 |
| $0.91 |
|
|
Summary: To compare two decimals, start at the left and compare digits in the same place-value position. It is helpful to write one decimal below the other. It is also easier to compare decimals when you have the same number of decimal digits. Thus, when comparing two decimals, we can write one or more extra zeros to the right of the last digit of one decimal so that both decimals have the same number of decimal digits.
Exercises
Directions: Compare each pair of decimals below using the symbols <. > or =. You may write one decimal below the other on paper to help you compare. Click once in an ANSWER BOX and type in your answer; then click ENTER. After you click ENTER, a message will appear in the RESULTS BOX to indicate whether your answer is correct or incorrect. To start over, click CLEAR.
1. |
Compare these decimals and enter <, > or = in the space provided.
|
2. |
Compare these decimals and enter <, > or = in the space provided.
|
3. |
Compare these decimals and enter <, > or = in the space provided.
|
4. |
Compare these decimals and enter <, > or = in the space provided.
|
5. |
Compare these decimals and enter <, > or = in the space provided.
|
 Example 1: Polygon Pizza Place caters children's parties with square-shaped pizza. Each pizza is exactly the same size and is divided into equal parts called slices. At Sam's party, each child had 2 out of 10 slices from a single pizza. At Elena's party, each child had 15 out of 100 slices from a single pizza. At which party did each child have more pizza?
Example 1: Polygon Pizza Place caters children's parties with square-shaped pizza. Each pizza is exactly the same size and is divided into equal parts called slices. At Sam's party, each child had 2 out of 10 slices from a single pizza. At Elena's party, each child had 15 out of 100 slices from a single pizza. At which party did each child have more pizza?



